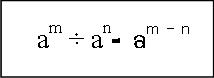ฐานความช่วยเหลือ เรื่องการหารร่วมมาก

ฐานความช่วยเหลือ เรื่องการหารร่วมมาก

ฐานความช่วยเหลือ เรื่องเลขยกกำลัง

ฐานความช่วยเหลือ เรื่องเลขยกกำลัง

สถานการณ์ เรื่องเลขยกกำลัง

         ครูแรม ครูประจำชั้นนักเรียนชั้นมัธยมศึกษาปีที่2 มีความคิดที่อยากให้นักเรียนรู้จักการประหยัดอดออมเงิน เพื่อที่จะนำเงินนั้นซื้อหนังสือคณิตศาสตร์ไปบริจาคให้โรงเรียนที่ขาดแคลนหนังสือเรียนวิชาคณิตศาสตร์ ที่มีราคาเล่มละ 86 บาท ซึ่งในห้องเรียนมีนักรียนทั้งหมด 35 คน ครูแรมจึงให้นักเรียนแต่ละคนนำเงินมาฝากเป็นเวลา 7 วัน
-วันแรก ครูแรมให้นำเงินมาออม 8 บาท
-วันที่สอง ให้ออมเงินเป็นสองเท่าของวันแรก
-วันที่สาม ให้ออมเงินเป็นสองเท่าของวันที่สอง
-วันที่สี่ ให้ออมเงินเป็นสองเท่าของวันที่สาม
-วันที่ห้า ให้ออมเงินเป็นสองเท่าของวันที่สี่
-วันที่หก ให้ออมเงินเป็นสองเท่าของวันที่ห้า
-วันที่เจ็ด ให้ออมเงินเป็นสองเท่าของวันที่หก
     เ มื่อครบทั้ง 7 วัน ครูแรมจึงให้นักเรียนรวมเงินของแต่ละคนที่ได้จากการออมและนำเงินของแต่ละคนมารวมกันให้ครบทั้ง 35 คน
      อยากทราบว่า นักเรียนหนึ่งคนเก็บเงินในระยะเวลา 7 วัน ได้เงินเท่าไรและเงินรวมของนักเรียน 35 คน สามารถซื้อหนังสือคณิตศาสตร์ได้กี่เล่ม

  

1.วิเคราะห์หาวิธีการคำนวณเงินของนักเรียน 1 คน ที่ได้จากการออมทั้ง 7วัน ว่าเป็นเงินเท่าใด พร้อมแสดงวิธีการคำนวณอย่างละเอียด

2.ในระยะเวลา7 วัน เงินรวมของนักเรียน 1 คน สามารถซื้อหนังสือคณิตศาสตร์ได้กี่เล่ม และเงินรวมของนักเรียนทั้งหมด 35 คน จะสามารถซื้อหนังสือคณิตศาสตร์ได้กี่เล่ม

ธนาคารความรู้ การคูณเลขยกกำลัง

      เลขยกกำลัง

           คือ การคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(aⁿ) จะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa)
  

    ตัวอย่าง
                  2⁵ เป็นเลขยกกำลัง ที่มี 2 เป็นฐานหรือตัวเลข และมี 5 เป็นเลขชี้กำลัง
    

    และ         2⁵   = 2x2x2x2x2  = 32

 

สมบัติของเลขยกกำลัง    

1. สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก          

                      

เช่น     2³x 2⁷x 2⁹ = 2 ^{(3 + 7 + 9)} = 2¹⁹

2. สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก

กรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > n 

                                                                    

เช่น     4¹²÷ 4³=4^12-3  = 4⁹

กรณีที่ 2 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, nเป็นจำนวนเต็มบวกที่ m = n

                                                                     

นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ a⁰ = 1

 เช่น      6⁷÷ 6⁷ = 6^7-7 = 6⁰  = 1  หรือถ้า (-7)^o = 1

 กรณีที่ 3เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m < n    

                                                                 

เช่น      =  1/ 5^4-9

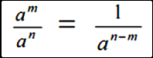
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว

             หรือ    

  เช่น               หรือ     

3.สมบัติอื่นๆของเลขยกกำลัง  

1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง                  

 เมื่อ a ≥0 และ m, n เป็นจำนวนเต็ม

เช่น              

                   

                     

2. เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ หรือการหารของจำนวนหลาย ๆจำนวน

      และ 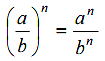        เมื่อ a ≠ 0 , b ≠ 0 และ n เป็นจำนวนเต็ม

เช่น                        

3. เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วน

       เมื่อ a > 0 และ n เป็นจำนวนเต็มบวกที่มากกว่า 1

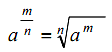เมื่อ a ≠ 0 และ m เป็นจำนวนเต็มบวก ; n ≥ 2

การใช้เลขยกกำลังแทนจำนวน

                การเขียนจำนวนที่มีค่ามากๆนิยมเขียนแทนได้ด้วยรูป Ax10ⁿเมื่อ 1≤A<10 และ n เป็นจำนวนเต็มบวก เช่น 16,000,000 = 1.6×10⁷ และทำนองเดียวกันการเขียนจำนวนเต็มที่มีค่าน้อยๆก็สามารถเขียนในรูป Ax10ⁿ ได้เช่นเดียวกัน  แต่ n จะเป็นจำนวนเต็มลบ เช่น 0.000016 = 1.6×10^-5

               หลักการเปลี่ยนจำนวนให้อยู่ในรูป Ax10ⁿ เมื่อ 1≤A<10 และ n เป็นจำนวนเต็มอย่างง่ายๆ คือให้พิจารณาว่าจุดทศนิยมมีการเลื่อนตำแหน่งไปทางซ้ายหรือขวากี่ตำแหน่ง ถ้าเลื่อนไปทางซ้ายเลขชี้กำลังจะเป็นบวก และถ้าเลื่อนไปทางขวาเลขชี้กำลังก็จะเป็นลบ

เช่น                   75000.0=7.5×10⁴     

                         0.000075 = 7.5×10^-5

หรือกล่าวได้ว่า ถ้าจุดทศนิยมเลื่อนไปทางขวา n ตำแหน่ง เลขชี้กำลังของ 10 จะลดลง n ถ้าจุดทศนิยมเลื่อนไปทางซ้าย n ตำแหน่ง เลขชี้กำลังของ10 จะเพิ่มขึ้น n

 

สรุป

          เลขยกกำลังเป็นการคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(aⁿ) หรือจะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa) อีกทั้งวิธีการคำนวณหาค่าเลขยกกำลังจะขึ้นอยู่กับสมบัติของเลขยกกำลังในแต่ละประเภทด้วย

การบวกเลขยกกำลัง

1.การบวกลบเลขยกกำลังที่มีฐานเหมือนกันและเลขยกกำลังเท่ากัน ให้นำสัมประสิทธิ์ของเลขยกกำลังมาบวกลบกัน

ตัวอย่าง                          

                       

2.การบวกลบเลขยกกำลังที่มีฐานเท่ากัน  แต่เลขยกกำลังไม่เท่ากันจะนำสัมประสิทธิ์มาบวกลบกันไม่ได้  ต้องทำในรูปของการแยกตัวประกอบ และดึงตัวประกอบร่วมออก

ตัวอย่าง         

                     

                      

หมายเหตุ 

       (-2)⁴ และ -2⁴ มีค่าไม่เท่ากันเพราะ  (-2)⁴ ฐานคือ  (-2)       

เลขชี้กำลังคือ 4 อ่านว่าลบสองทั้งหมดยกกำลังสี่มีค่าเท่ากับ 16

       -2⁴  ฐานคือ 2 เลขชี้กำลังคือ 4 อ่านว่าลบของสองกำลังสี่มีค่าเท่ากับ  -16

ธนาคารความรู้ เรื่อง การหารร่วมมาก

 

ตัวเลขจำนวนเต็มใด ๆ ก็ตามที่มีค่ามากกว่า 1 สามารถเขียนในรูปของตัวประกอบที่เป็นจำนวนเฉพาะได้

ถ้าให้ n เป็นเลขจำนวนเต็มที่มีค่ามากกว่า 1

                n = p₁ⁿ₁ p₂ⁿ₂…p_kⁿ_k

เมื่อ p คือเลขจำนวนเฉพาะ
        p₁ < p₂ < … < p_k
          n₁, n₂, n₃, …n_k เป็นเลขจำนวนเต็ม > 0
            k >= 1

ตัวอย่างเช่น
                                       28 = 2² x 5⁰ x 7¹
                         

                           200 = 2³ x 5² x 7⁰

ห.ร.ม. คืออะไร

“สมมุติเลิศชายมีกระดาษแผ่นหนึ่ง มีลักษณะเป็นรูปสี่เหลี่ยมพื้นผ้า กว้าง 8 นิ้ว ยาว 12 นิ้ว เลิศชายต้องการตัดกระดาษนี้ให้เป็นรูปสี่เหลี่ยมจัตุรัสรูปเล็ก ๆ หลายรูป และให้ได้ขนาดรูปสี่เหลี่ยมจัตุรัสขนาดใหญ่ที่สุด โดยไม่มีกระดาษเหลือเศษ”

 ลองดูจากตัวอย่างง่าย ๆ ตัวอย่างหนึ่ง
 

จากตัวเลข  8 = 23 x 30
จากตัวเลข  12 = 22 x 30

  เห็นได้ชัดว่า ตัวเลขทั้งสองตัวเขียนอยู่ในรูปจำนวนเฉพาะได้

ตัวเลขจำนวนเฉพาะที่ตรงกัน และพิจารณาส่วนของตัวที่ซ้ำกันน้อยที่

 เช่น มี 2 ซ้ำกันน้อยที่สุด 2 ตัว (2²)

 มี 3 ซ้ำกันน้อยที่สุด 0 ตัว (3⁰)

  ตัวหารร่วมที่หารเลข 8 และ 12 ลงตัวที่มากที่สุดคือ 2² x 3⁰ = 4

  4 จึงเป็นตัวหารร่วมของด้านทั้งสอง

  นั่นคือหากตัดแบ่งเป็นรูปสี่เหลี่ยมจัตุรัสให้ด้านละ 4 จะได้สี่เหลี่ยมจัตุรัสใหญ่สุด
แบ่งได้  6 รูป

หลักการ ห.ร.ม.

          สมมุติว่าเรามีตัวเลขจำนวนเต็มบวกสองตัว a และ b เราจะหาตัวหารร่วมได้อย่างไร

ถ้าสมมุติให้ d เป็นตัวหารร่วม

                                                        d หาร a ได้ลงตัว

                                                        d หาร b ได้ลงตัว

ถ้าเขียนจำนวน a และ b ในรูปแบบเลขจำนวนเฉพาะ

                                                        a = p₁^a₁ p₂^a₂ … p_k^a_k
                                                                  b = p₁^b₁ p₂^b₂ … p_k^b_k
                                                          โดยที่ a_i, b_i >= 0
 

เมื่อ d หาร a และ b ลงตัว เขียน d ในรูปแบบจำนวนเฉพาะ
                                                                 d = p₁^d₁ p₂^d₂ … p_k^d_k
                                                                เมื่อ d_i <= a_i
                                                                      d_i <= b_i
                                                                      d_i <= min(a_i, b_i)

                            หรืออาจกล่าวได้ว่า d_i น้อยกว่าค่าน้อยสุดระหว่าง a_i, b_i
        แต่ถ้าจะให้เป็นตัวหารร่วมที่มากที่สุด (ห.ร.ม.) ค่า d_i จะต้องเท่ากับค่าน้อยที่สุดระหว่าง a_i, b_i
                                                                d_i = min(a_i, b_i)

วิธีการหา  ห.ร.ม.
            1.  โดยการแยกตัวประกอบ  มีิวิธีการดังนี้
                       (1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหาร ห.ร.ม.
                       (2) เลือกตัวประกอบที่ซ้ำกันของทุกจำนวนมาคูณกัน
                       (3) ห.ร.ม. คือ  ผลคูณที่ได้
             
                   ตัวอย่าง   จงหา ห.ร.ม. ของ  56   84  และ 140
             วิธีทำ            56 =
                                84 =
                              140 =
                              เลือกตัวที่ซ้ำกัน  ที่อยู่ทั้ง 56 84และ 140 ตัวทีซ้ำกันเอามาซ้ำละ 1 ตัว   
                                                    คือ  มีเลข  2   เลข  2 และ เลข 7

                 ดังนั้น       ห.ร.ม.   =  

  คุณสมบัติ

ตัวหารร่วมของ a และ b จะเป็นตัวหารของ gcd (a, b)gcd (a, b) เมื่อ a และ b ไม่เป็นศูนย์พร้อมกัน จะเป็นจำนวนเต็มบวก d ที่น้อยที่สุดที่สามารถเขียนในรูป d = a·p + b·q เมื่อ p และ q เป็นจำนวนเต็ม จำนวน p และ q สามารถคำนวณได้จากอัลกอริทึมของยุคลิดเพิ่มเติมถ้า a หาร b·c ลงตัว และ gcd (a, b) = d แล้ว a/d หาร c ลงตัวถ้า m เป็นจำนวนเต็มใดๆแล้ว gcd (m·a, m·b) = m·gcd (a, b) และ gcd (a + m·b, b) = gcd (a, b) ถ้า m เป็นตัวหารร่วมของ a และ b แล้ว gcd (a/m, b/m) = gcd (a, b) /m

ห.ร.ม.เป็นฟังก์ชันการคูณ กล่าวคือ ถ้า a₁ และ a₂ เป็นจำนวนเฉพาะสัมพัทธ์แล้ว gcd (a₁·a₂, b) = gcd (a₁, b) ·gcd (a₂, b)

ห.ร.ม.ของจำนวนสามจำนวน หาได้จาก gcd (a, b, c) = gcd (gcd (a, b) , c) = gcd (a, gcd (b, c)) นั่นคือ ห.ร.ม.มีสมบัติการเปลี่ยนหมู่

gcd (a, b) นั้นมีความเกี่ยวข้องกับตัวคูณร่วมน้อย lcm (a, b) : จะได้ว่า

gcd (a, b) ·lcm (a, b) = a·b.

สูตรนี้มักถูกใช้เพื่อคำนวณค่าคูณร่วมน้อย โดยเริ่มด้วยการหา ห.ร.ม. โดยใช้อัลกอริทึมของยุคลิด จากนั้นหารผลคูณของตัวเลขทั้งสองด้วย ห.ร.ม. คุณสมบัติการกระจายด้านล่างนี้เป็นจริง:

gcd (a, lcm (b, c)) = lcm (gcd (a, b) , gcd (a, c))

lcm (a, gcd (b, c)) = gcd (lcm (a, b) , lcm (a, c)).

การนิยามให้ gcd (0, 0) = 0 และ lcm (0, 0) = 0 นั้นมีประโยชน์เนื่องจากจะทำให้เซตของจำนวนธรรมชาติเป็นแลตทิซแบบกระจายที่บริบูรณ์ โดยที่ ห.ร.ม. เป็นการดำเนินการ meet และ ค.ร.น. เป็นการดำเนินการ join การขยายนิยามนี้สอดคล้องกับนัยทั่วไปของนิยามสำหรับริงสลับที่ด้านล่าง

ในระบบพิกัดคาร์ทีเซียน gcd (a, b) สามารถตีความว่าเป็นจำนวนของจุดที่มีพิกัดเป็นจำนวนเต็มบนเส้นตรงที่เชื่อมจุด (0, 0) และจุด (a, b) โดยที่ไม่นับจุด (0, 0)

ตัวอย่าง   จงหา ห.ร.ม. ของ  56   84  และ 140
                         วิธีทำ      2)  56       84       140
                                      2)  28       42        70
                                      7)  14       21        35
                                            2         3         5

                           ห.ร.ม.  คือ  2 x 2 x 7 = 28

 ประโยชน์ของ  ห.ร.ม.
            1. ใช้ทอนเศษส่วนใ้ห้เป็นเศษส่วนอย่างต่ำ
            2. ใช้คำนวณการแบ่งสิ่งของที่มีจำนวนไม่เท่ากันออกเป็นส่วนๆ  ที่เท่าักันโดยไม่ปะปนกันและให้เป็นจำนวนที่มากที่สุด